
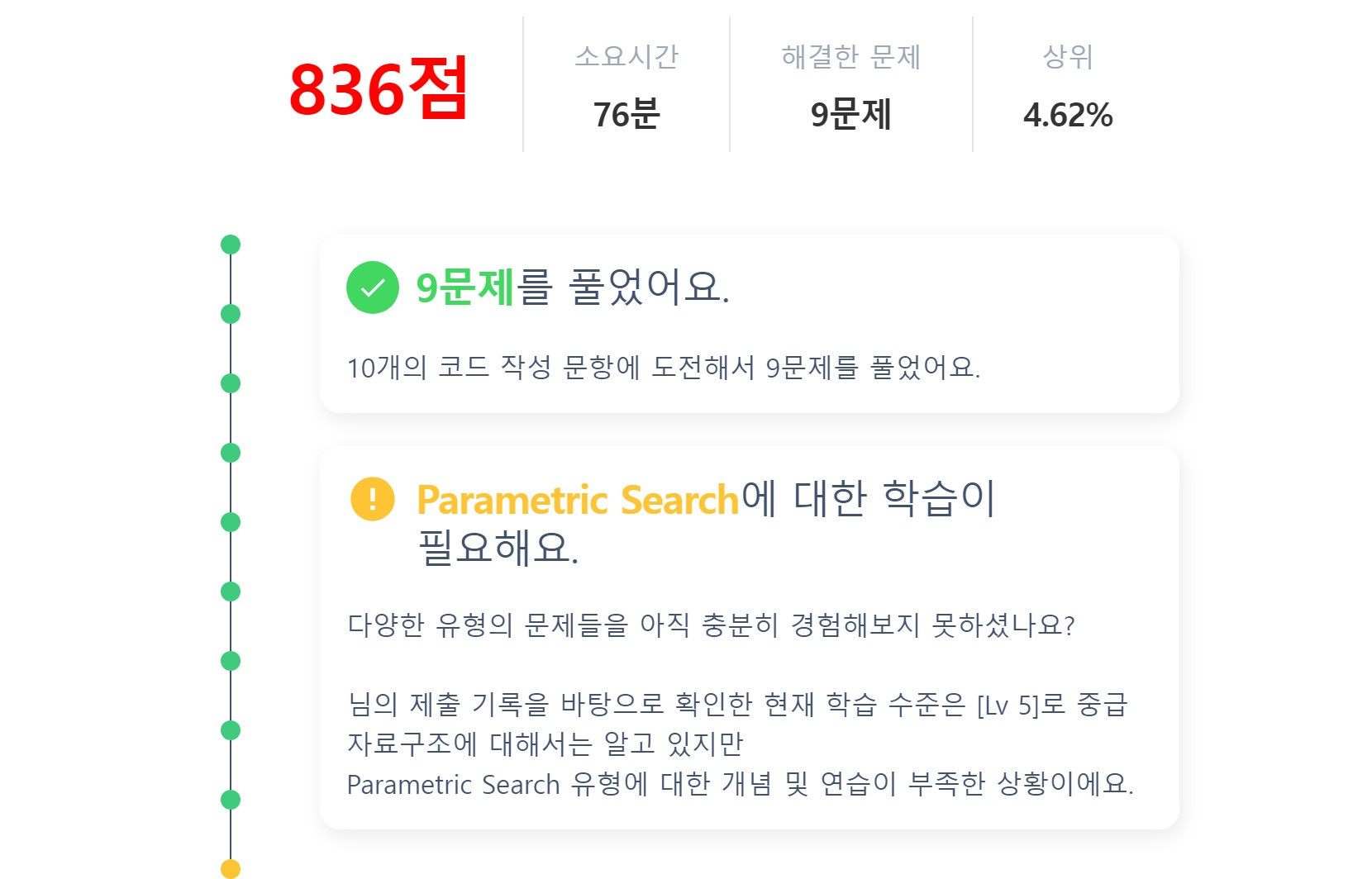
실력진단 결과
코드트리 8주차 실력진단 결과
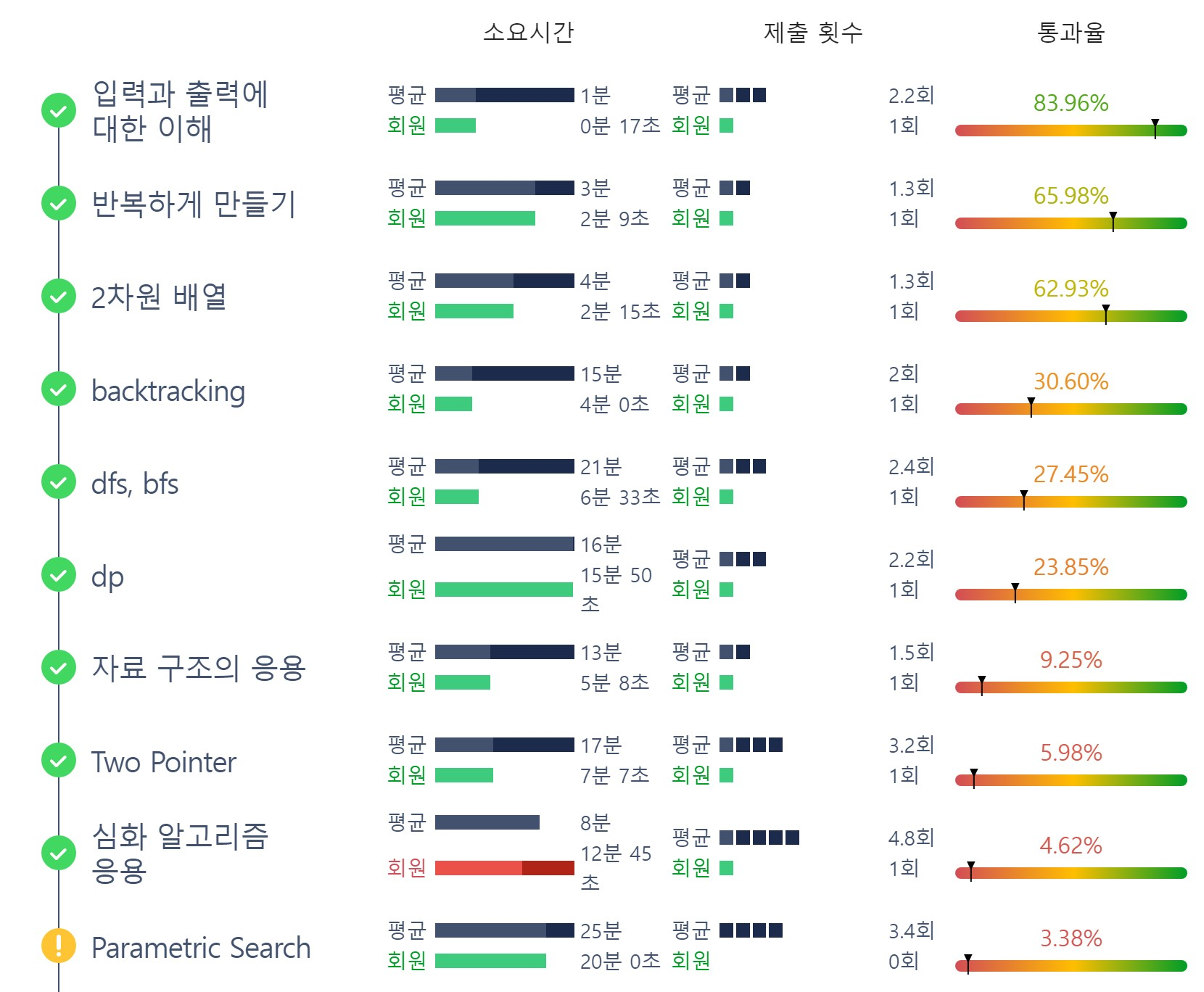
오늘의 학습
Parametric Search
다음 문제는 어떻게 해결해 볼 수 있을까요?
1부터 n까지의 자연수의 합이 100이상인 경우 중
가능한 n의 최솟값을 구하는 프로그램을 작성해보세요.
단, 답은 1에서 30사이라고 가정합니다.
무작정 코드를 작성한다면, 1, 2, 3 ..., 30 전까지 계속 더해보며 최초로 그 합이 100을 넘는 순간을 찾아 바로 그 직전의 숫자를 구하게 될 것입니다. 넘어야 하는 합을 s라 했을 때 시간복잡도는 O(S)가 됩니다.
하지만 만약 이 문제가 수학 문제로 나왔다면, 다음과 같이 시도하게 될 것입니다.
1차 시도 (n = 15)
1부터 15까지의 합은 120이므로, 일단 15은 답의 후보 중 하나입니다.
이제 더 작은 값도 가능한지 [1 ~ 14] 사이를 조사해보려고 합니다.
2차 시도 (n = 7)
1부터 7까지의 합은 28이므로, n은 분명히 7보다 커져야 합니다.
이제 더 좋은 경우가 있을지 [8 ~ 14] 사이를 조사해보려고 합니다.
3차 시도 (n = 11)
1부터 11까지의 합은 66이므로, n은 분명히 11보다 커져야 합니다.
이제 더 좋은 경우가 있을지 [12 ~ 14] 사이를 조사해보려고 합니다.
4차 시도 (n = 13)
1부터 13까지의 합은 91이므로, n은 13보다 커져야 합니다.
이제 [14 ~ 14] 사이를 조사해보면 됩니다.
5차 시도 (n = 14)
1부터 14까지의 합은 105이므로, 14도 답의 후보 중 하나가 됩니다.
더 이상 탐색할 범위가 없으므로, 가능했던 후보 15, 14 중 최솟값인 14가 답이 됩니다.
이렇듯 5번 만에 문제에서 원하는 답을 구할 수 있게 됩니다. 이게 어떻게 가능한 걸까요?
잘 생각해보면, 이 문제는 n이 커질수록 1부터 n까지의 합이 커진다는 특성을 가지고 있습니다. 즉, x축을 n, y축을 1부터 n까지의 합이라고 했을 때 다음과 같은 그림이 만들어지게 됩니다.
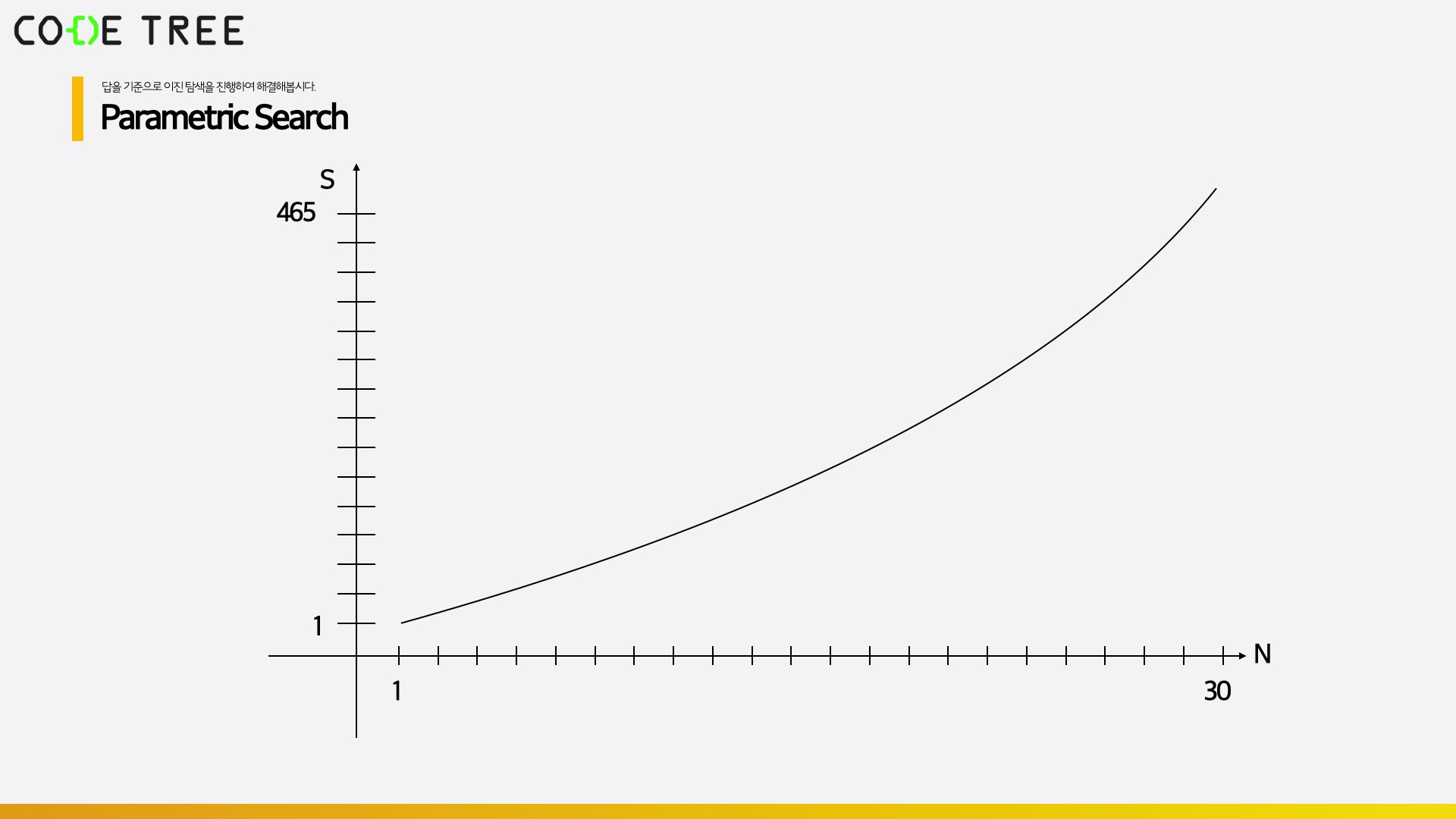
이 그림에서 조건을 만족하는 n들 중 (1부터 n까지의 합이 100 이상인 경우) 최솟값을 구해야 합니다.
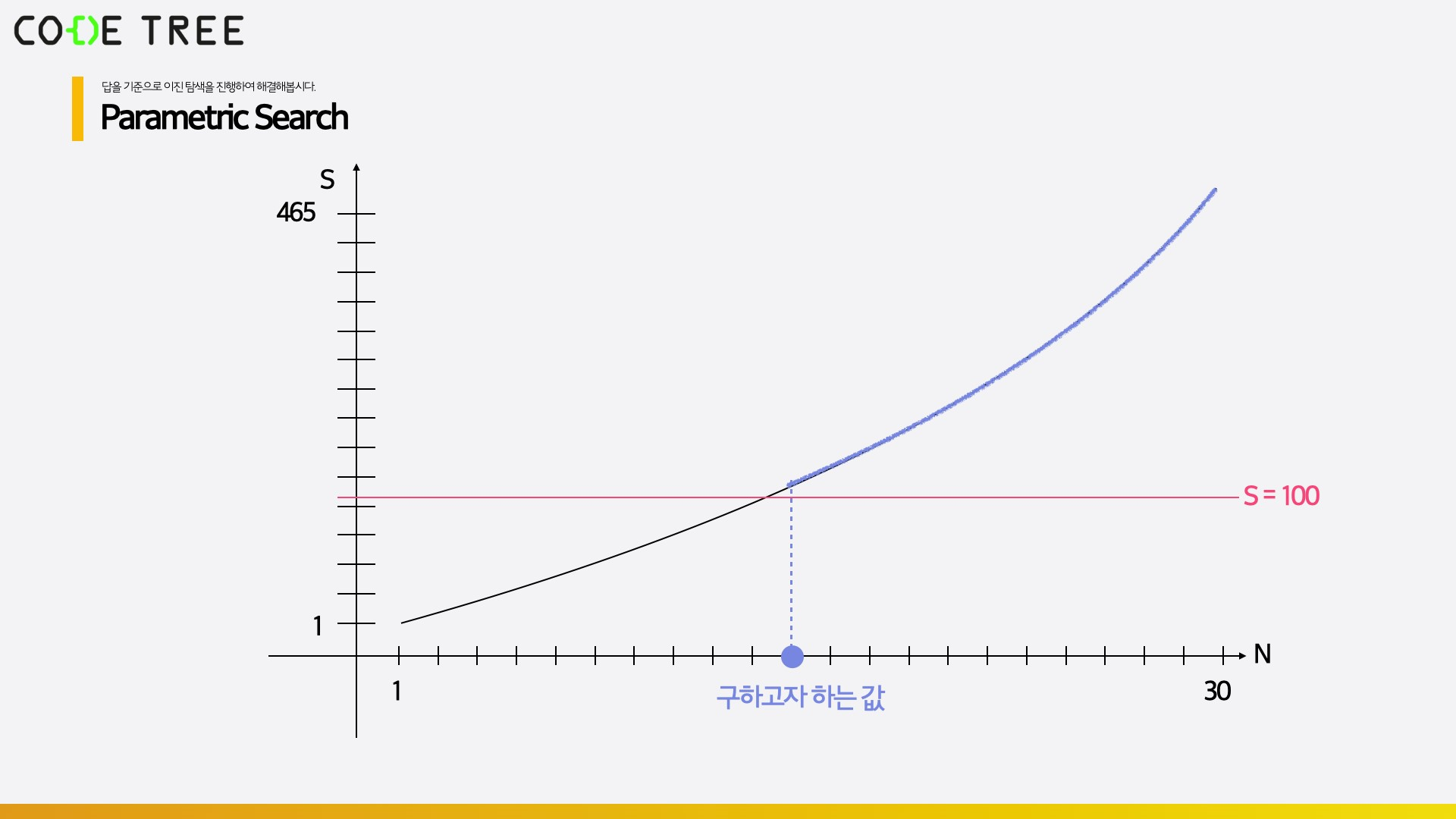
가능한 범위는 1에서 30 사이이므로 일단 전부 조건을 충족시킬 가능성이 있습니다.
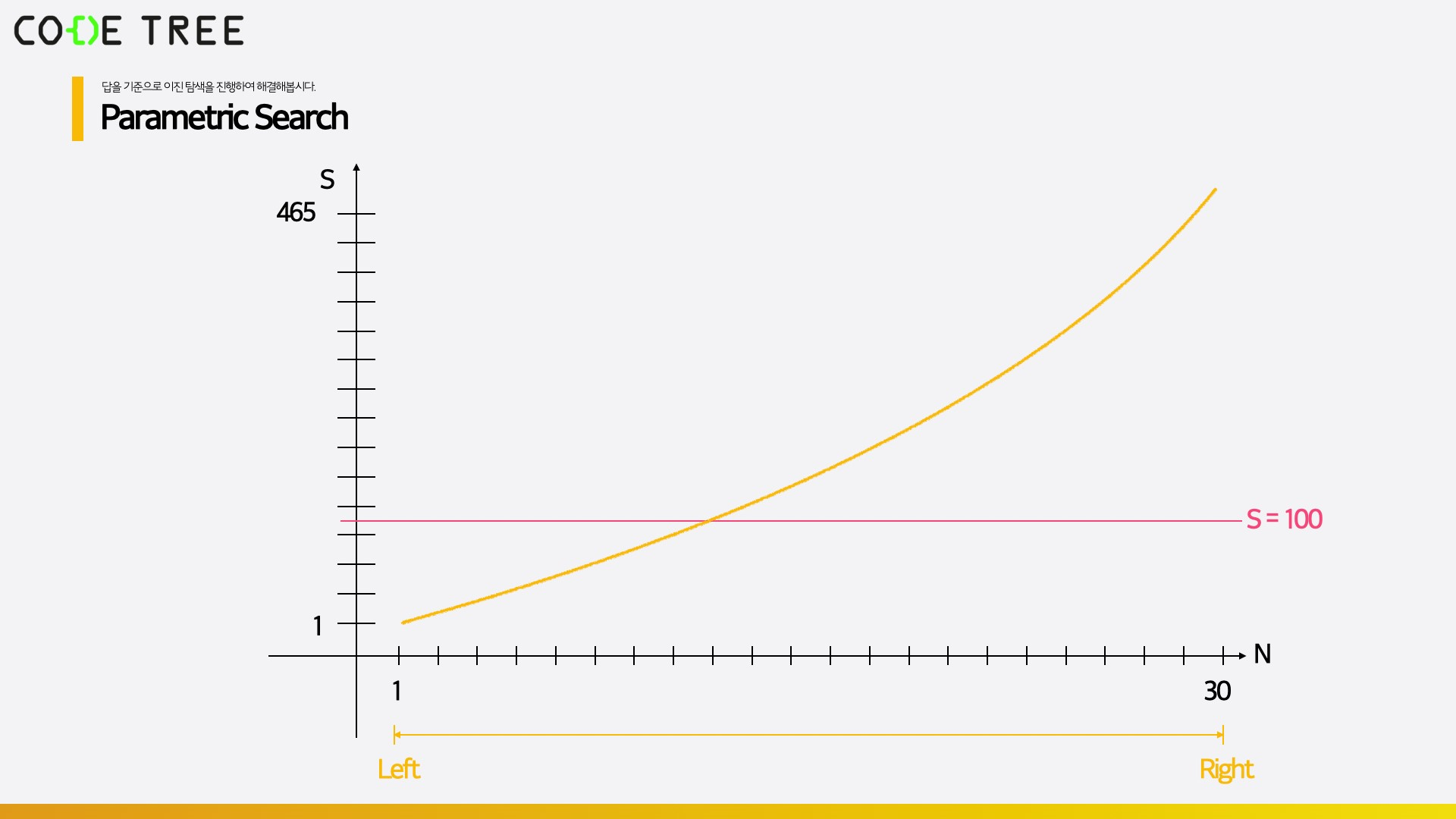
먼저 n이 15이었을 때를 확인해봅니다. 1부터 15까지의 합은 120이므로 이미 조건을 만족하기 때문에, 조건을 만족하는 경우 중 최솟값을 구해야 하는 이 문제에서는 n이 16보다 큰 경우를 더 이상 탐색해야 할 필요가 없습니다. 따라서 n=15는 답의 후보가 되며, 그 다음 탐색 범위는 [1, 14]가 됩니다.
이제 n이 1과 14의 가운데 값인 7이었을 경우를 확인해봅니다. 1부터 7까지의 합은 28이므로 n은 조건을 만족시키기 위해 분명히 7보다 커져야 합니다. 따라서 7보다 작은 경우는 전부 버리게 되고, 그 다음 탐색 범위는 [8 ~ 14]가 됩니다.
다음에는 n이 8과 14의 가운데 값인 11이었을 경우를 확인해봅니다. 1부터 11까지의 합은 66이므로 n은 조건을 만족시키기 위해 분명히 11보다 커져야 합니다. 따라서 11보다 작은 경우는 전부 버리게 되고, 그 다음 탐색 범위는 [12 ~ 14]가 됩니다.
다음에는 n이 12과 14의 가운데 값인 13이었을 경우를 확인해봅니다. 1부터 13까지의 합은 91이므로 n은 조건을 만족시키기 위해 분명히 13보다 커져야 합니다. 따라서 13보다 작은 경우는 전부 버리게 되고, 그 다음 탐색 범위는 [14 ~ 14]가 됩니다.
마지막으로 n이 14인 경우를 확인해봅니다. 1부터 14까지의 합은 105이므로, 14도 답의 후보 중 하나가 됩니다.
더 이상 탐색할 범위가 없으므로, 가능했던 후보 15, 14 중 최솟값인 14가 답이 됩니다.
이처럼 답이 절대 될 수 없는 범위는 버리고, 답이 되는 범위에서는 가능한 답 중 문제에서 원하는 조건(여기서는 최솟값)에 맞는 답을 계속 찾아가주면 됩니다. 이러한 경우에는 이번 문제에서처럼 x 값이 증가함에 따라 y값이 같이 계속 증가하거나, 계속 감소하는 형태에서 이진 탐색을 진행하여 문제에서 원하는 답을 구할 수 있습니다. 이렇게 답을 기준으로 이진탐색을 진행하는 방식을 Parametric Search 라고 부릅니다.
코드 개형은 다음과 같습니다. 이 문제에서 원하는 답은 합이 100 이상인 경우 중 최솟값 입니다. 따라서 최솟값을 구하기 위해서는 minNum이라는 변수를 활용해 초기값으로 답이 될 수 없는 최댓값인 31을 넣어놓고 문제를 해결합니다. 이는 Lower Bound, Upper Bound를 계산하는 코드와 많이 유사합니다.
public class Main {
public static void main(String[] args) {
int left = 1;
int right = 30;
int minNum = 31;
while (left <= right) {
int mid = (left + right) / 2;
if((1)) {
(2)
}
else {
(3)
}
}
System.out.print(minNum);
}
}이제 minNum 값이 갱신되는 순간이 언제인지를 생각해봅니다. minNum은 정의상 mid * (mid + 1) / 2이 100보다 크거나 같은 경우에 대해 가능한 mid 값들 중 최솟값이 되어야 합니다.
따라서 (1) 위치에 mid * (mid + 1) / 2 >= 100 조건을 걸어줍니다. 왼쪽에 조건을 만족하는 mid값이 더 있을 수 있으므로 right값을 움직여줘야 하며, 이 경우 minNum을 현재까지의 최솟값인 minNum과 mid를 비교하여 둘 중 더 작은 값으로 넣어줘야 합니다. 이처럼 답의 후보가 되는 범위를 항상 if 조건에 넣어 처리한다는 생각으로 코드를 작성하시면 됩니다.
조건을 만족하지 않는 경우에는 left값을 움직여주면 됩니다. 따라서 코드는 다음과 같이 작성이 가능합니다.
public class Main {
public static void main(String[] args) {
int left = 1; // 가장 작은 숫자 값을 설정합니다.
int right = 30; // 가장 큰 숫자 값을 설정합니다.
int minNum = 31; // 최소이므로, 답이 될 수 있는 값보다 더 큰 값으로 설정합니다.
while (left <= right) { // [left, right]가 유효한 구간이면 계속 수행합니다.
int mid = (left + right) / 2; // 가운데 위치를 선택합니다.
if(mid * (mid + 1) / 2 >= 100) { // 1부터 n까지의 합이 100보다 같거나 크다면
right = mid - 1; // 왼쪽에 조건을 만족하는 숫자가 더 있을 가능성 때문에 right를 바꿔줍니다.
minNum = Math.min(minNum, mid);// 답의 후보들 중 최솟값을 계속 갱신해줍니다.
}
else
left = mid + 1; // 100보다 작은 경우라면 left를 바꿔줍니다.
}
System.out.print(minNum); // 조건을 만족하는 최소 n 값을 출력합니다.
}
}
'Problem Solving > CodeTree' 카테고리의 다른 글
| [코드트리 챌린지] 7주차 (0) | 2023.10.20 |
|---|---|
| [코드트리 챌린지] 6주차 (1) | 2023.10.13 |
| [코드트리 챌린지] 5주차 (0) | 2023.10.05 |
| [코드트리 챌린지] 4주차 (0) | 2023.10.03 |
| [코드트리 챌린지] 3주차 (0) | 2023.09.25 |
