
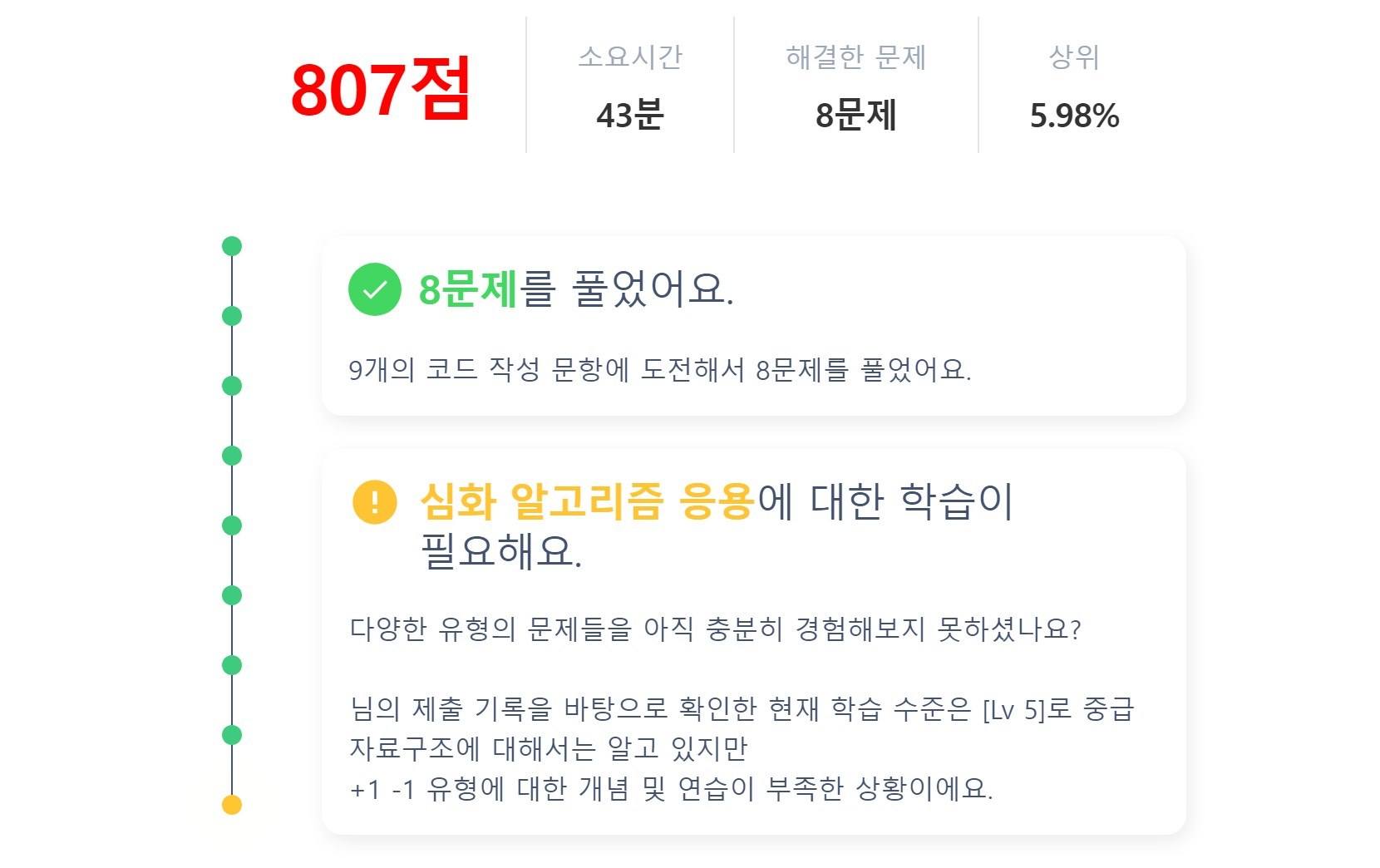
실력진단 결과
코드트리 6주차 실력진단 결과
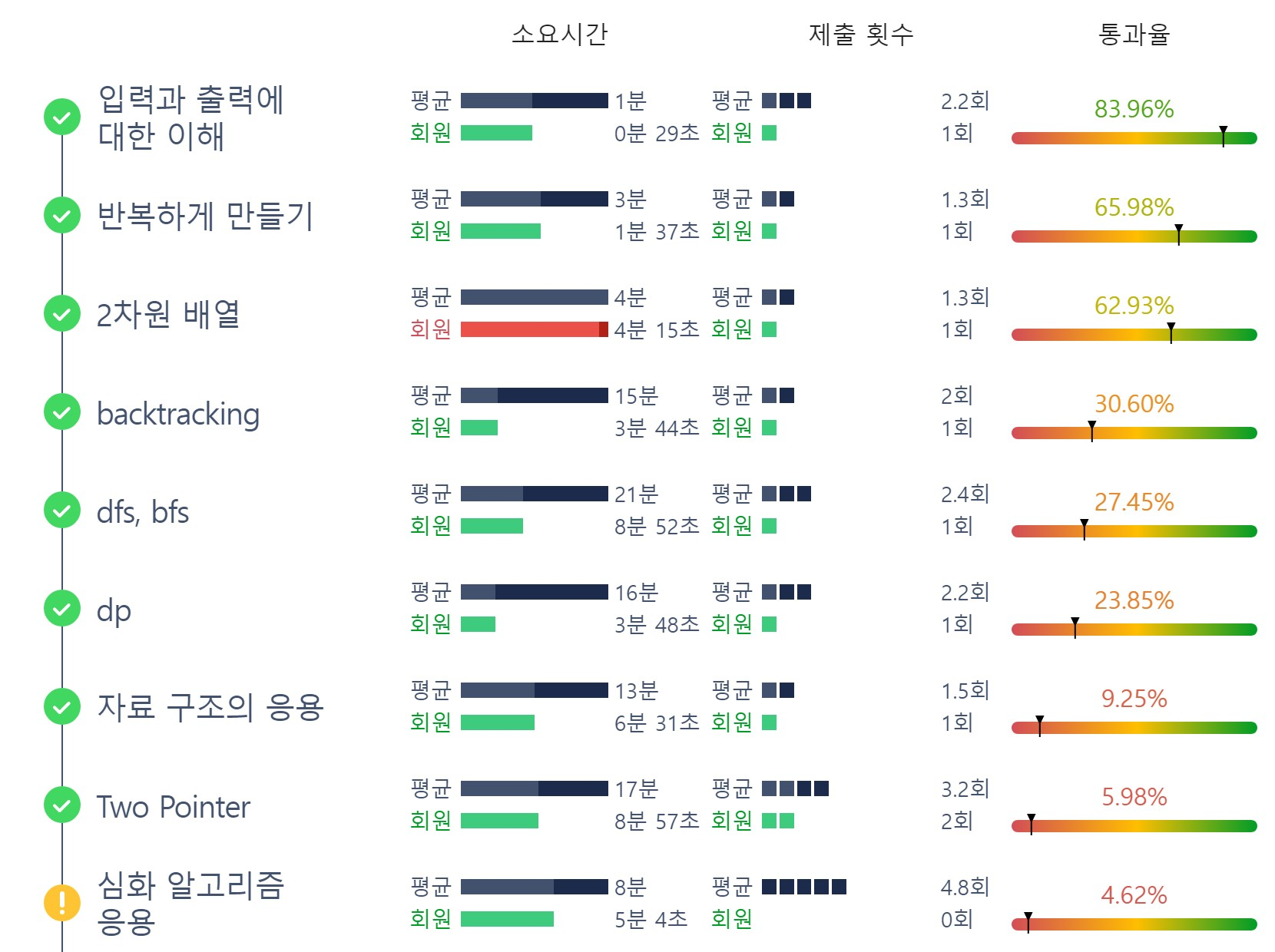
오늘의 학습
Bitmask DP
다음 문제는 어떻게 해결해볼 수 있을까요?
아래와 같이 노드가 4개 간선이 x개 있는 양방향 그래프가 주어져있습니다.
3번 노드에서 시작하여 모든 노드를 정확히 한번씩만 방문하되, 이동거리의 합이 최소가 되도록 해보세요.
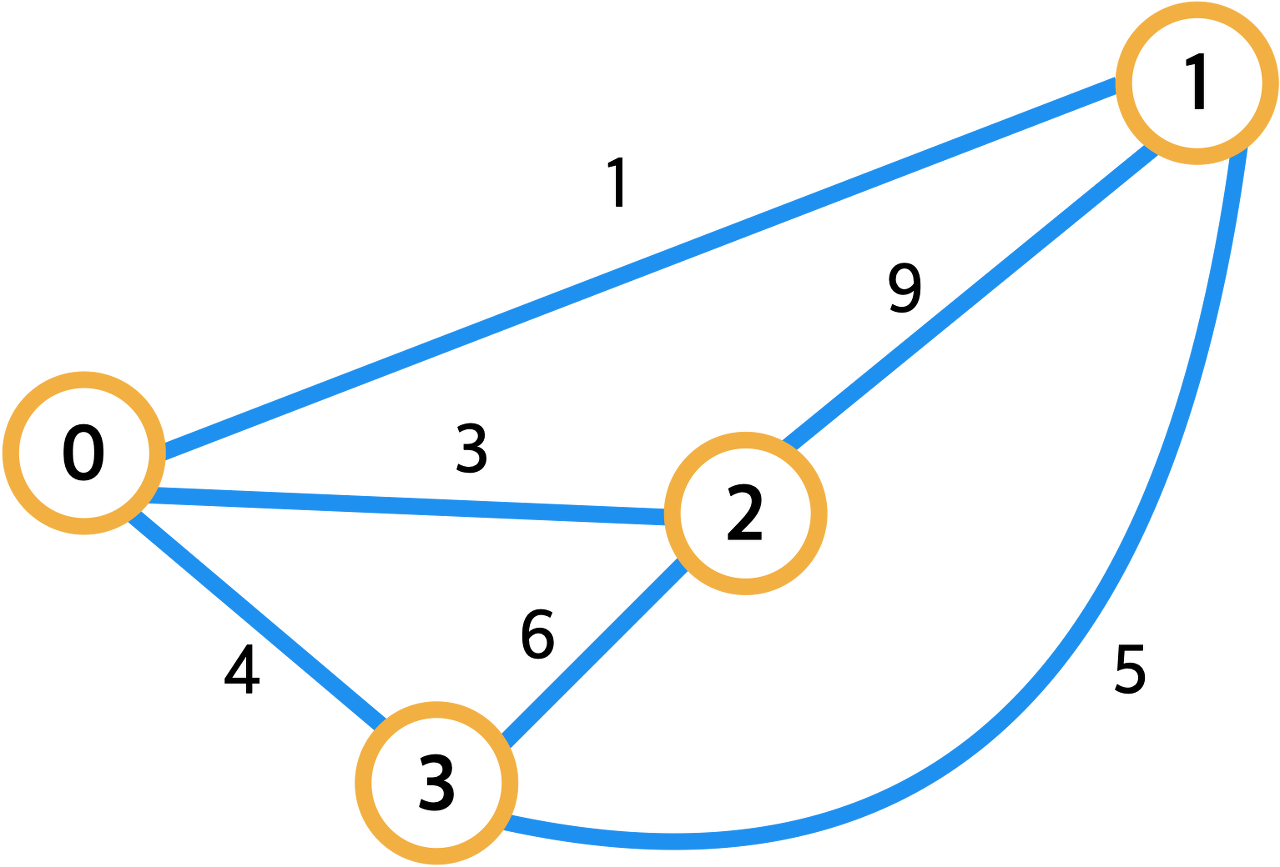
3번에서 시작하여 모든 정점을 단 한번씩만 방문해야 하는 문제이므로 가장 간단한 방법은 모든 순열을 만들어보는 백트래킹을 이용하는 것입니다. 백트래킹을 이용해 모든 순열을 만드는 방법에 대해 아직 잘 모르신다면, 순열 만들기 유형을 공부하시고 나서 다시 이 설명을 읽는 것을 추천드립니다.
수열 만들기 링크 : https://www.codetree.ai/missions/2/problems/n-permutation/introduction
백트래킹을 이용한 코드는 아래와 같습니다. 가능한 모든 순열을 만들어야 하므로 시간복잡도는 O(N!)이 됩니다.
public class Main {
public static final int n = 4;
public static int[][] dist = new int[][]{
{0, 1, 3, 4},
{1, 0, 9, 5},
{3, 9, 0, 6},
{4, 5, 6, 0},
};
public static boolean[] visited = new boolean[n];
public static int ans = (int)1e9;
// 지금까지 cnt개의 정점을 방문했고
// 현재 위치 x에 있고
// 지금까지의 이동거리의 합이 sumDist라 했을 때
// 모든 정점을 방문하기 위한 시뮬레이션을 진행하여
// 그 중 최적의 값을 구합니다.
public static void findMax(int cnt, int x, int sumDist) {
// 종료조건입니다.
if(cnt == n) {
ans = Math.min(ans, sumDist);
return;
}
for(int i = 0; i < n; i++) {
if(visited[i])
continue;
visited[i] = true;
findMax(cnt + 1, i, sumDist + dist[x][i]);
visited[i] = false;
}
}
public static void main(String[] args) {
// 3번 지점에서 시작하여
// 최적의 답을 구합니다.
visited[3] = true;
findMax(1, 3, 0);
System.out.print(ans);
}
}이 문제는 bimask DP를 이용하여 O(2^N ×N^2 )에도 해결해볼 수 있습니다.
3번 정점에서 시작하여 (1) 지금까지 방문한 노드의 종류가 아예 동일하고, (2) 동시에 현재 서있는 노드의 위치가 동일하고, (3) 지금까지의 이동거리가 동일한 경우 즉, 예로 아래와 같이 두 상황은 아예 동등한 상황이라고 생각해볼 수 있습니다.

따라서 이 문제는 (1) 지금까지 방문한 노드의 종류가 동일하고, (2) 현재 서있는 노드의 위치가 동일한 상태에서 이동거리를 최소화하는 DP로 해결이 가능합니다.
dp[i][j]를 3번을 시작으로 겹치지 않게 방문한 위치에 해당하는 상태가 i이고 그래서 현재 서 있는 위치가 j가 되었을 때 가능한 최소 이동 거리가 됩니다. 이때 방문한 위치들에 해당하는 상태를 나타내는 i는 구현의 편의를 위해 bitmask를 이용하여 하나의 정수값으로 나타낼 수 있습니다. 아직 bitmask에 대해 잘 모른다면, bitmask 유형을 공부하시고나서 다시 이 설명을 읽는 것을 추천드립니다. 여기서는 3번을 시작으로 겹치지 않게 방문한 위치를 x1, x2, ..., xk라 헀을 때 2^x1 + 2^x2 + ... + 2^xk 값이 i가 됩니다.
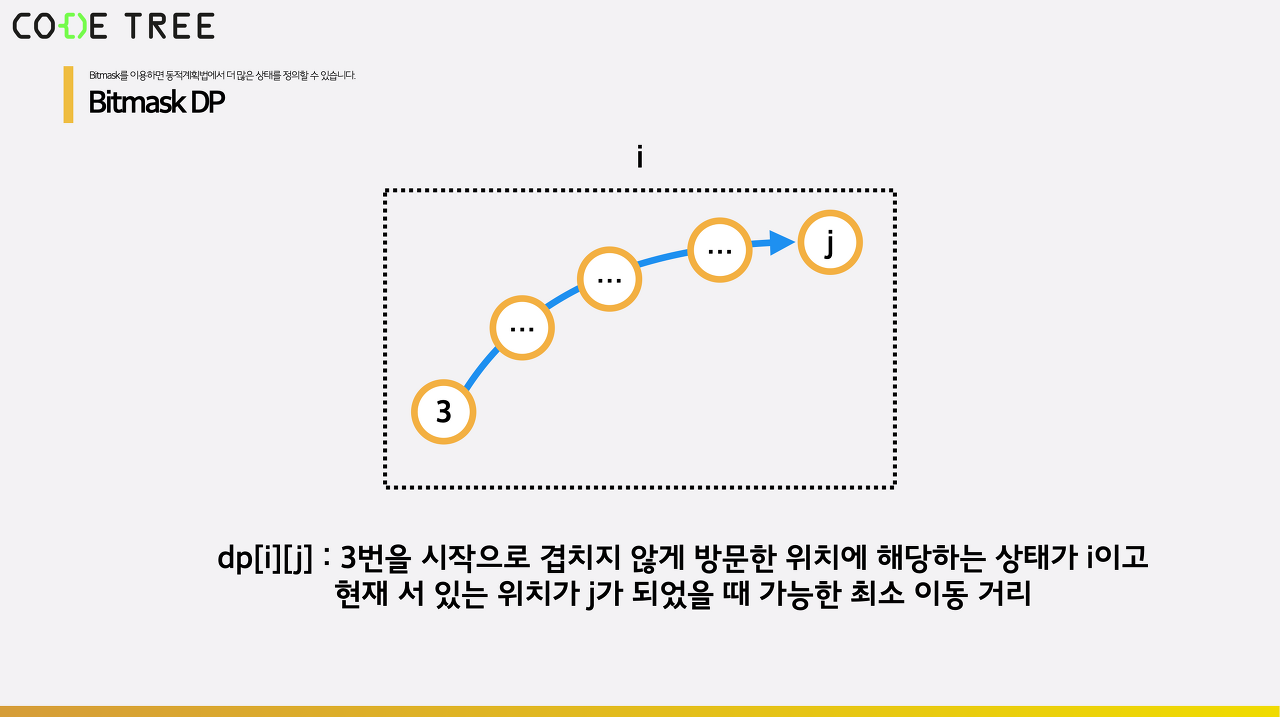
이제 여기서 점화식을 세우기 보다는 뿌려지는 형태의 동적계획법을 진행해보려고 합니다. 보통의 동적계획법 문제는 점화식을 세워 작은 문제에 해당하는 이전 값들이 채워져있다는 가정 하에서 현재 상태에 해당하는 최적의 값을 계산하는 식으로 진행됩니다. 이러한 방식은 이미 완성된 값을 가져오는 형태의 동적계획법입니다. 하지만 상황에 따라 가져와야 할 부분을 직관적으로 떠올리거나 정리하는 것이 어려운 경우가 더러 있습니다. 지금 이 문제에서는 점화식을 세워 가져오는 방법으로 진행하기보다는, 이미 값이 구해져있다는 가정 하에서 이 상태가 영향을 미치는 그 다음 상태를 찾아 값을 갱신해주는 식인 뿌려지는 형태의 동적계획법을 진행해보려고 합니다.
dp[i][j]값이 이미 구해져있다고 가정해보겠습니다. 이제 그 다음 위치로 k번 정점으로 간다고 한다면, 지금까지 방문한 상태의 bitmask 값은 i+2^k 가 되고 마지막 방문 위치는 k가 되기에 아래와 같이 아직 방문하지 않은 모든 정점에 대해 값을 갱신해주면 됩니다.
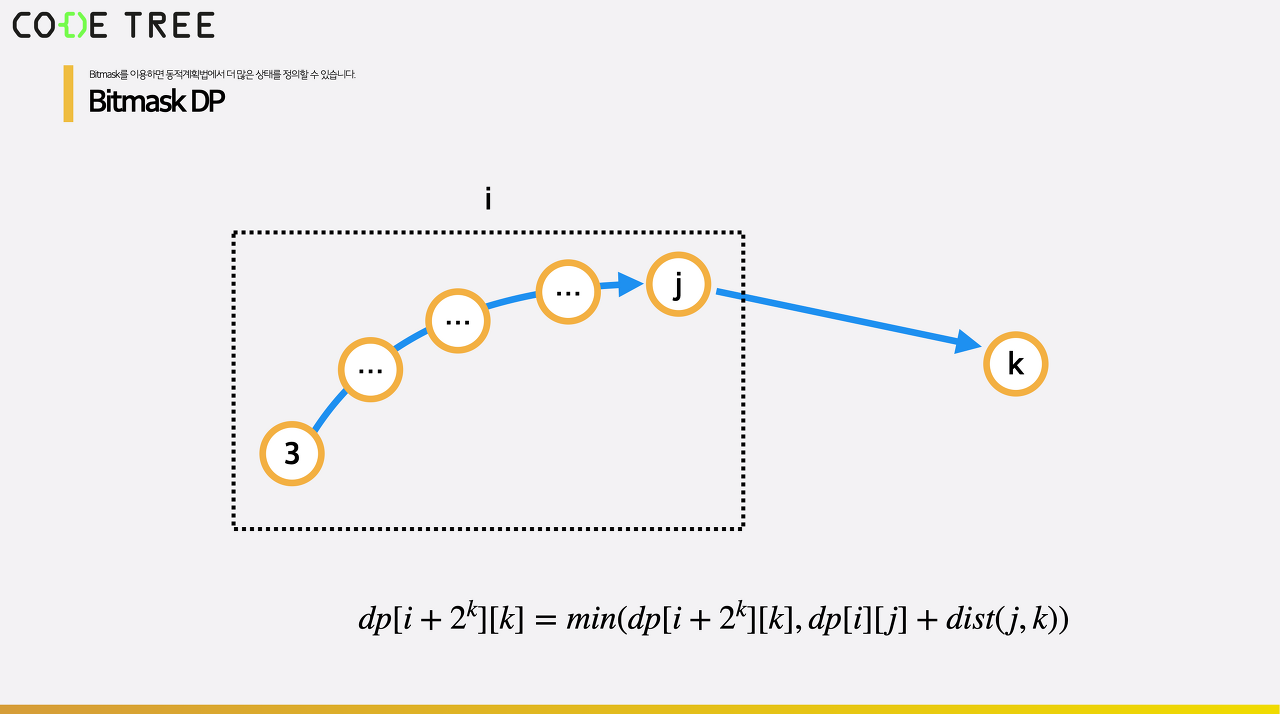
초기조건은 3번 지점을 시작으로 하며 현재 3번 위치에 서있으며 지금까지의 이동거리가 0이므로 dp[8(=1000)][3] = 0이 됩니다.
이제 점화식에 따라 값을 갱신하면 됩니다. 이때 dp는 특성상 더 작은 문제부터 값이 채워져야 하는 것이 중요합니다. 이를 쉽게 작성하기 위해서는 그저 i값을 0부터 전부 채워져 있는 값인 2^4 −1(=1111) 까지 1씩 증가하며 진행하면 됩니다. 그 이유는 i가 증가하는 순으로 bitmask를 확인하면 해당 bit보다 더 작은 케이스는 이미 다 고려가 되었음을 보장할 수 있기 때문입니다.
이제 순서대로 dp값을 채우는 과정을 살펴보면 아래와 같습니다.
값을 채운 뒤 답은 모든 정점을 방문한 상태 중 가능한 최소 이동거리가 됩니다. 즉, 어디에서 끝나는지는 전혀 상관이 없는 문제이기에 dp[2^4 −1(=1111)][i] 값 중 최솟값이 답이 됩니다. 이 풀이에서 dp의 상태는 O(2^N ∗N)개 이며, 각 상태에 대해 그 다음 정점에 해당하는 곳을 탐색하기 위해 O(N)개를 보게 되므로 총 시간복잡도는 O(2^N ∗N^21)이 됩니다. n이 커질수록 백트래킹으로 구현했을 때의 O(N!)에 비해 훨씬 빠른 시간복잡도를 갖는 방법이라 할 수 있습니다.
이 문제의 풀이 관련 코드는 아래와 같습니다.
public class Main {
// 변수 선언
public static final int n = 4;
public static int[][] dist = new int[][]{
{0, 1, 3, 4},
{1, 0, 9, 5},
{3, 9, 0, 6},
{4, 5, 6, 0},
};
// dp[i][j] :
// 3번을 시작으로 겹치지 않게 방문한 위치를
// x1, x2, ..., xk라 헀을 때
// 2^x1 + 2^x2 + ... + 2^xk 값이 i이고 (bitmask된 정수값이 i)
// 그래서 현재 서 있는 위치가 j가 되었을 때
// 가능한 최소 이동거리
public static int[][] dp = new int[1 << n][n];
public static void main(String[] args) {
// 최소 이동거리를 구하는 문제이기에
// 초기값으로 아주 큰 값을 넣어줍니다.
for(int i = 0; i < (1 << n); i++)
for(int j = 0; j < n; j++)
dp[i][j] = (int)1e9;
// 초기조건은
// 3번 지점을 시작으로 하며 현재 3번 위치에 서있으며
// 지금까지 이동한 거리가 0인 상태인
// dp[8][3] = 0이 됩니다.
dp[8][3] = 0;
// 뿌려주는 방식의 dp를 진행합니다.
// dp[i][j]가 계산이 되어있다는 가정하에서
// 그 다음 상태값을 갱신합니다.
for(int i = 0; i < (1 << n); i++) {
for(int j = 0; j < n; j++) {
// j번 지점을 방문한게 정의상 불가능 하다면
// 패스합니다.
if(((i >> j) & 1) == 0)
continue;
// 현재 j번에서 그 다음 위치로 k번 지점을 가게 되는 경우
// 상태값을 계산하여 최솟값을 갱신해줍니다.
for(int k = 0; k < n; k++) {
// k번 지점을 이미 방문한 적이 있다면
// 중복 방문은 조건상 불가하므로 패스합니다.
if(((i >> k) & 1) == 1)
continue;
// j번에서 k번으로 가는 길이 없다면
// 패스합니다.
if(dist[j][k] == 0)
continue;
dp[i + (1 << k)][k] = Math.min(
dp[i + (1 << k)][k], dp[i][j] + dist[j][k]
);
}
}
}
// 어디서 끝나던 상관이 없기 때문에
// 모든 지점을 방문한 경우 중 최솟값을 갱신합니다.
int ans = (int)1e9;
for(int i = 0; i < n; i++)
// 최솟값을 갱신합니다.
ans = Math.min(ans, dp[(1 << n) - 1][i]);
System.out.print(ans);
}
}'Problem Solving > CodeTree' 카테고리의 다른 글
| [코드트리 챌린지] 8주차 (1) | 2023.10.26 |
|---|---|
| [코드트리 챌린지] 7주차 (0) | 2023.10.20 |
| [코드트리 챌린지] 5주차 (0) | 2023.10.05 |
| [코드트리 챌린지] 4주차 (0) | 2023.10.03 |
| [코드트리 챌린지] 3주차 (0) | 2023.09.25 |
