
실력진단 결과
코드트리 3주차 실력진단 결과
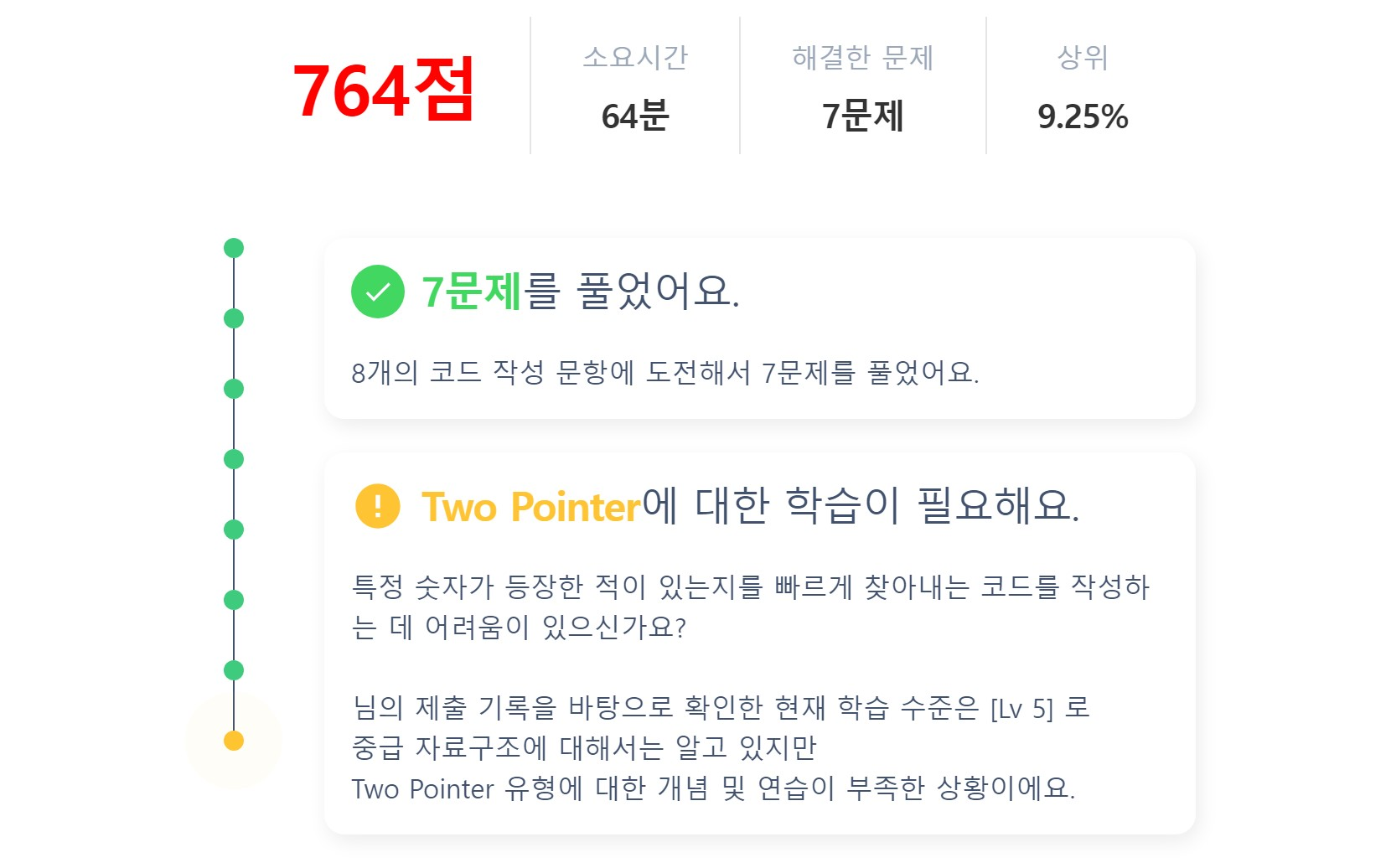

오늘의 학습
Two Pointer & 두 포인터
다음 문제는 어떻게 해결해 볼 수 있을까요?
[6, 3, 2, 4, 9, 1] 와 같이 숫자들이 주어졌을 때, 특정 구간을 잘 골라 구간 내 숫자의 합이 10을 넘지 않으면서 가장 큰 구간의 크기를 구하는 프로그램을 작성해보세요.
무작정 코드를 작성한다면, 모든 구간 O(N^2)개를 잡아보면서 그 안에 있는 숫자를 전부 더해 합이 10을 넘지 않는 경우 중 구간 크기의 최댓값을 구하면 되므로 O(N^3)이 소요됩니다.
이 방법에 대한 코드는 다음과 같습니다.
public class Main {
public static void main(String[] args) {
int[] arr = new int[]{0, 6, 3, 2, 4, 9, 1};
int k = 10;
int n = 6;
// 가능한 구간 중 최대 크기를 구합니다.
int ans = 0;
// 모든 구간을 탐색합니다.
for(int i = 1; i <= n; i++) {
for(int j = i; j <= n; j++) {
// 구간 내 합을 구합니다.
int sumVal = 0;
for(int l = i; l <= j; l++)
sumVal += arr[l];
// 구간 내 합이 10 이하라면,
// 구간 크기 중 최댓값을 갱신합니다.
if(sumVal <= k)
ans = Math.max(ans, j - i + 1);
}
}
// 조건을 만족하는 가장 큰 구간의 크기는
// [3, 2, 4]로 3이 됩니다.
System.out.print(ans);
}
}이때 구간을 정한 뒤 구간 내 합을 구할 것이 아니라, 구간 내 시작점 i를 정하고 시작점 i로부터 합이 10을 넘지 않는 가장 멀리 있는 구간의 끝 j를 정하는 식으로 진행한다면, O(N^2)으로도 문제에서 원하는 최대 구간의 크기를 구할 수 있습니다.
이 방법에 대한 코드는 다음과 같습니다.
public class Main {
public static void main(String[] args) {
int[] arr = new int[]{0, 6, 3, 2, 4, 9, 1};
int k = 10;
int n = 6;
// 가능한 구간 중 최대 크기를 구합니다.
int ans = 0;
// 모든 구간을 탐색합니다.
for(int i = 1; i <= n; i++) {
// 구간 내 합이 10을 넘지 않을때까지 계속 진행합니다.
int sumVal = 0;
for(int j = i; j <= n; j++) {
sumVal += arr[j];
// 구간 내 합이 10을 넘게되면 그만 진행합니다.
if(sumVal > k)
break;
// 현재 구간 [i, j]는
// 유효한 구간이므로
// 구간 크기 중 최댓값을 갱신합니다.
ans = Math.max(ans, j - i + 1);
}
}
// 조건을 만족하는 가장 큰 구간의 크기는
// [3, 2, 4]로 3이 됩니다.
System.out.print(ans);
}
}그런데 구간의 시작점 i가 고정되었을 때, 최대로 뻗어 나갈 수 있는 구간의 끝 j를 전부 살펴보았을 때 어떤 규칙이 보이지 않으신가요?
그렇습니다. i가 1씩 늘어날 때마다, 최대로 뻗어나갈 수 있는 j의 위치는 항상 같거나 증가한다는 것을 확인할 수 있습니다!
그 이유를 생각해보면 지극히 당연합니다. i가 1이 증가하면 합이 Ai값만큼 감소하기 때문에 그만큼 더 뒤로 이동할 수 있는 여유 공간이 생기기 때문입니다.
이렇듯 문제에서의 특정 조건에 의해 원하는 구간의 양 끝을 나타내는 2개의 포인터가 한 방향으로만 계속 전진하는 형태의 테크닉을 Two Pointer라고 부릅니다.
Two Pointer를 이용해 i가 1증가했을 때 j는 이전 값에서 시작하여 감소시키지 않고 뻗어나갈 수 있는 최대로 뻗어나가도록 진행을 하면, i, j 모두 한 방향으로만 진행하기 때문에 시간복잡도가 O(N)이 됩니다.
Two Pointer로 이 문제를 해결한 코드는 다음과 같습니다. 실제 2중 포문으로 작성되어 있지만, i, j 모두 한 반향으로만 진행하기 때문에 시간복잡도가 두 for loop의 곱이 아닌, 합으로 나타내짐에 꼭 유의해야 합니다.
public class Main {
public static void main(String[] args) {
int[] arr = new int[]{0, 6, 3, 2, 4, 9, 1};
int k = 10;
int n = 6;
// 가능한 구간 중 최대 크기를 구합니다.
int ans = 0;
// 구간을 잡아봅니다.
int sumVal = 0;
int j = 0;
for(int i = 1; i <= n; i++) {
// 구간 내 합이 10을 넘지 않을때까지 계속 진행합니다.
while(j + 1 <= n && sumVal + arr[j + 1] <= k) {
sumVal += arr[j + 1];
j++;
}
// 현재 구간 [i, j]는
// i를 시작점으로 하는
// 가장 긴 구간이므로
// 구간 크기 중 최댓값을 갱신합니다.
ans = Math.max(ans, j - i + 1);
// 다음 구간으로 넘어가기 전에
// arr[i]에 해당하는 값은 구간에서 제외시킵니다.
sumVal -= arr[i];
}
// 조건을 만족하는 가장 큰 구간의 크기는
// [3, 2, 4]로 3이 됩니다.
System.out.print(ans);
}
}
'Problem Solving > CodeTree' 카테고리의 다른 글
| [코드트리 챌린지] 6주차 (1) | 2023.10.13 |
|---|---|
| [코드트리 챌린지] 5주차 (0) | 2023.10.05 |
| [코드트리 챌린지] 4주차 (0) | 2023.10.03 |
| [코드트리 챌린지] 2주차 (0) | 2023.09.18 |
| [코드트리 챌린지] 1주차 (0) | 2023.09.17 |
